sisällysluetteloon
seuraavaan
edelliseen
Matematiikka, kauneus ja taide
Matematiikan kauneus
Marcel Duchamp, Pariisin šakkimestari vuodelta 1932, korosti sattuman osuutta tässä pelissä, jossa periaatteessa ei ole sijaa sattumalle. Hänen pelitapaansa on kuvattu näin:
»Duchampin vääräoppinen näkemys pelistä yhdistyneenä hänen rakkauteensa erityisen kauniita šakkiyhdistelmiä kohtaan – mikä joskus sai hänet ottamaan tarpeettoman suuria riskejä – voi olla syynä hänen moniin häviöihinsä. – – taiteilija Duchampissa hukutti alleen šakinpelaajan – jopa turnauksissa.» (Schwarz)
Oli riskien kanssa niin tai näin, Duchamp puhui toisinaan šakkipelin kauneudesta: hän kutsui šakkipeliä »mekaaniseksi veistokseksi» ja mainitsi että siinä »luodaan kauniita ongelmia». »Kauneus šakissa ei näytä olevan visuaalinen kokemus niin kuin maalauksessa. Šakin kauneus on lähempänä runouden kauneutta – –.»
Tähän tapaan kauneus tai esteettinen arvo usein liitetään šakkipeliin. Brittiesteetikko Harold Osborne onkin valmis kutsumaan šakkia taidelajiksi, koska »muun ohella se tarjoaa mahdollisuuden sellaisten älyllisten kohteiden luomiseen, joille on tyypillistä kauneus», ja koska juuri taiteessa »kauneus ja sen tarkastelu ovat lopullisena päämääränä». – Voitaisiin jopa väittää, että kauneus kuuluu šakkipelin päämääriin, koska turnauksissa jaetaan kauneuspalkintoja peleille ja siirtoyhdistelmille. Arvosteluperusteina ovat tällöin oikeellisuus, taloudellisuus, vaikeus, yllättävyys ja omaperäisyys, monipuolisuus ja vaihtelevuus sekä looginen yhtenäisyys.
Toiset eivät ole yhtä avaramielisiä kuin Osborne. Michael Lipton, R. Matthews ja John Rice julkaisivat 1960-luvulla kirjan šakkitehtävistä alaotsikkona »Johdatus taiteenlajiin». Heidän mielestään šakkipeli on yhtä epätaiteellista kuin parlamenttiväittely, kun taas šakkitehtävä on kuin runo. Nykyaikainen šakkitehtävän laatija ei pyri keskiaikaisen edeltäjänsä tavoin vaikeuteen vaan »ilmaisemaan taiteellisia ideoita šakin muodossa». Kirjoittajien mukaan »hyvä tanssi, hyvä ruoka tai hyvä jalkapallo eivät tarkasti ottaen ole varsinaisia taiteenlajeja» kun taas »parhaat šakkitehtävät, baletti tai taloarkkitehtuuri ovat». Šakkitehtävät »tarjoavat saman syvän tunnun taiteellisesta nautinnosta, saman tajun taloudellisuudesta, siitä että keinot päämäärän saavuttamiseksi on pelkistetty minimiin» kuin taiteen suurteokset, sellaiset kuin John Donnen runo Kuume, Tizianin maalaus Vuorisaarna ja Beethovenin Suuri fuuga. Šakkitehtävät ovat joillekin ihmisille helpommin lähestyttäviä ja voivat siksi toimia kuin portaina suuren taiteen ymmärtämiseen: »ja äkkiä ymmärtää, kuinka paljon suuri taiteilija voi tehdä kovin vähällä».
Suomalaiset Osmo Kaila ja Matti Myllyniemi puolestaan määrittelevät, että »tehtävä- eli taideshakissa» tehtävän
»on oltava ratkaisultaan yksimääreinen (= korrekti), rakenteeltaan mahdollisimman taloudellinen ja aistikas sekä sisällykseltään omaperäinen».
Heidän mukaansa lajista »pystyy nauttimaan jo alkuasteella», mutta »täydelliset taidenautinnot – – saa vasta asiantuntija».
| Lisätietoa: Seuraavat seikat on noukittu Suomen tehtäväniekat ry:n kotisivuilta: Shakkitehtävä on shakkiasema, johon liittyy jokin kysymys. Esim. perinteisessä mattitehtävässä pitää keksiä, miten valkean on pelattava, jotta musta saadaan mattiin tietyssä siirtomäärässä. Shakkitehtävän on aina joku laatinut, se ei ole pelitilanne oikeasta pelistä. Tehtäväaseman on oltava laillinen eli pelin alkuasemasta sääntöjen mukaisin siirroin saavutettavissa. Tehtävän asema esitetään yleensä shakkikuviossa, jonka alla on siihen liittyvä kysymys eli tehtävän vaatimus. Kuvion päällä on tehtävän laatijan nimi sekä tiedot siitä, missä tehtävä on ensimmäisen kerran julkaistu. Shakkitehtävään on ainoastaan yksi ratkaisu. Jos tehtävään löytyy muitakin ratkaisuja, kuin tekijän tarkoittama, on tehtävässä sivuratkaisu, joka pilaa tehtävän. Esimerkkinä olkoon G. E. Carpenterin laatima tehtävä, joka on julkaistu Dubuque Chess Journalissa v. 1873. Tehtävä: Miten tehdä matti kahdella siirrolla? 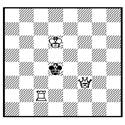 Ratkaisu: Alkusiirto on Df3-h3. Sen jälkeen mustan on pelattava Kd4-e4, ja valkea tekee matin siirrolla Tc3-c4. 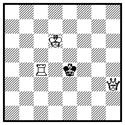 |
*
Šakki tai šakkitehtävät kuuluvat siis joidenkin mielestä taiteen piiriin. Tämä ajatus ei liene yhtä yleisesti hyväksytty kuin se, että šakki on matematiikkaa, osa tuota tieteiden kuningattareksi ylistettyä oppialaa, jota toiset eivät ole pitäneet tieteenä lainkaan – tarkoittaen ettei se ole fysiikkaan, kemiaan tai biologiaan verrattavaa luonnontiedettä. Vaikka šakki on matematiikkaa, se ei ole korkeatasoista vaan » ›triviaalia› matematiikkaa», niin kuin brittimatemaatikko G. H. Hardy asian ilmaisi. Hänen mukaansa »paras matematiikka on sekä vakavaa että kaunista», kun taas šakkitehtävien »kauneus on suhteellisen alhaisella tasolla», ja ne ovatkin siksi »ikään kuin matematiikan virsiä».
Jos esteettistä arvoa pidetään tärkeänä, saattaa šakkipeli viedä šakkitehtävien äärelle ja ne taas varsinaiseen matematiikkaan, jota Hardy siis luonnehti sekä vakavaksi että kauniiksi. Usein matematiikan kauneudesta puhutaan tähän tapaan selviönä asettamatta asiaa kyseenalaiseksi. Melkoisen tuore on teos Kauneimmat matemaattiset kaavat, jossa »tavoite on paljastaa matemaattisten kaavojen kauneus». Jo Aristoteleen mukaan ne erehtyvät, »jotka väittävät, että matemaattiset tieteet eivät puhu mitään kauniista», ja hän jatkoi:
»Kauniin pääasiallisimmat muodot ovat järjestys [taxis], symmetria [symmetria] ja määräytyneisyys [horismenon], joita matemaattiset tieteet erityisesti ilmaisevat.»
Francis Hutcheson ja älyllinen kauneus
Estetiikan historiassa matemaattista tai älyllistä kauneutta ei ole paljon tutkittu. Jossain määrin asiaan paneutui 1700-luvulla elänyt britti Francis Hutcheson. Hänen mukaansa ›kauneus› merkitsee »meissä syntyvää ideaa», ja kysymykseen »mikä tämän idean synnyttää?» hän vastasi: ne rakenteet tai kuviot »joissa on yhdenmukaisuutta vaihtelevuudessa» (uniformity amidst variety).
Tätä vaihtelevan ykseyden ajatusta Hutcheson sitten soveltaa myös matematiikkaan ja luonnontieteisiin – joskus väkinäisestikin, kuten väittäessään että »tasasivuisen kolmion kauneus on vähäisempi kuin neliön», koska ne ovat yhtä yhtenäisiä mutta neliö on moniosaisempi ja siten vaihtelevampi. Järkevämmältä Hutchesonin ajattelu vaikuttaa, kun hän puhuu teorioista ja teoreemoista. Hän kutsuu niitä seuraavassa ›löydöiksi› (discovery) ja väittää, että ne – toisin kuin yksittäiset »totuudet» – voivat olla kauniita:
»Verratkaamme tällaisten löytöjen tuottamaa tyydytystä siihen ahdistuneeseen mielentilaan, joka syntyy kun – – teemme kokeita, joita emme kykene pelkistämään minkään yleisen säännön alaisiksi, vaan kasaamme vain joukoittain yksityisiä hajanaisia havaintoja. Kussakin näistä kokeista löydetään uusi totuus, mutta mukaan ei liity mielihyvää tai kauneutta, vaikka kokonaisuus onkin vaihteleva, ennen kuin kykenemme löytämään jonkinlaista ykseyttä tai pelkistämään koetulokset jonkin yleisen säännön alaisiksi.»
Kauneimpia ovat kaikkein yleisimmät väittämät, niissä
»näemme hämmästyttävää vaihtelevuutta ja samalla yhdenmukaisuutta, mikä herättää suurta mielihyvää, joka on riippumaton mahdollisuudesta saada lisäetuja».
Yhteen laajaan totuuteen sisältyy tällöin suuri joukko yksittäisiä totuuksia:
»Väitteissä on – – kauneutta, kun yksi teoreema sisältää suuren joukon seurausväitteitä, jotka voidaan helposti johtaa siitä. – – Sellainen on Eukleideen ensimmäisen kirjan 35. teoreema, josta johdetaan koko suoraviivaisten alueiden mittaaminen hajottamalla ne kolmioiksi – – Luonnontutkimuksessa on samantapaista kauneutta tiedossa, joka koskee suuria periaatteita tai yleispäteviä voimia ja josta seuraa lukemattomia vaikutuksia. Sellainen on painovoima Sir Isaac Newtonin järjestelmässä.»
Kun puhutaan matematiikan (tai luonnontieteen) kauneudesta, on Hutchesonin jälkeenkin ollut tavallista viitata sellaisiin asioihin kuin ykseyteen ja monipuolisuuteen tai niin kuin Aristoteles sanoi »järjestykseen» ja »symmetriaan» (jolla hän tarkoitti harmoniaa). Nämä ovatkin piirteitä, joihin vetoamalla esteettistä arvoa voidaan perustella: »Miksi pidät tuota kauniina?» »Siinä on niin paljon saatu mahdutetuksi niin vähään.» »Se on niin yksinkertainen ja samalla monitahoinen.» »Kokonaisuus on niin järjestynyt ja harmoninen.»
Millaista matematiikan kauneus voi olla?
Puhe matemaattisesta kauneudesta tuo lähinnä mieleen »elegantin» todistelman tai »siististi» ratkaistun matemaattisen ongelman. Bertrand Russell kirjoittaakin:
»Kauneimmissa aikaansaannoksissa esitellään todisteluketju, jossa jokainen rengas on tärkeä, jossa kauttaaltaan vallitsee tuntu helppoudesta ja kirkkaudesta ja jossa premissien perustalta päästään johonkin mitä ei olisi voinut uskoa mahdolliseksi ja lisäksi tavalla, joka vaikuttaa luonnolliselta ja väistämättömältä.»
Tällaisesta elegantista todistelmasta on usein tarjottu esimerkiksi, kuinka Eukleides osoittaa, että alkulukuja (eli jaottomia kokonaislukuja) on ääretön määrä. Victor Papanek kirjoittaa asiasta seuraavasti (kutsuen alkulukuja jaottomiksi luvuiksi):
»Jonkin asian yksinkertaisuuden tuottamaa tyydytystä voidaan kutsua eleganssiksi. Kun puhumme ›elegantista› ratkaisusta, tarkoitamme jotakin tietoisesti kehitettyä, jotakin jossa monimutkainen muuttuu yksinkertaiseksi: // Esimerkiksi sopii matematiikan alalta Euklideen todistus siitä, että jaottomien lukujen määrä on rajaton: Jaottomat luvut ovat sellaisia, joita ei voida jakaa tasan kokonaisluvulla, kuten esim. 3, 17, 23 jne. Saattaisi olettaa, että mitä korkeammalle numerosarjassa tulemme, sitä harvinaisemmiksi jaottomat luvut käyvät, koska yhä useammat pienet luvut voivat tällöin esiintyä niiden tekijöinä, ja että lopuksi tulisimme johonkin erittäin suureen lukuun, joka olisi numeroiden viimeinen neitsyt, suurin jaoton luku. // Euklideen todistus osoittaa yksinkertaisesti ja elegantisti, että näin ei ole ja että vaikka jatkaisimme kuinka tähtitieteellisiin lukuihin tahansa, löytäisimme aina sellaisia, jotka eivät ole pienempien tuloja, vaan ikäänkuin neitseellisesti syntyneitä. Tässä on todistus: olettakaamme, että P olisi suurin jaoton luku; kuvitelkaamme sitten luku, joka olisi 1 * 2 * 3 * 4 * ... * P. Tämän luvun merkintänä on symboli (P!). Tähän lukuun lisätään sitten 1: (P! + 1). Tämä luku ei tietenkään ole jaollinen P:llä tai millään P:tä pienemmällä luvulla (koska ne kaikki sisältyvät P!:hen); näin ollen (P! + 1) on joko P:tä suurempi jaoton luku taikka sillä on P:tä suurempi jaoton tekijä ... m.o.t. // Tämän todistuksen herättämä suuri tyydytys on sekä esteettistä että intellektuaalista: se on eräänlaista lähes täydellisen aiheuttamaa lumousta.»
Olkoon toinen esimerkki geometrian alalta. Pythagoraan lauseen mukaan suorakulmaisen kolmion hypotenuusan neliö on kateettien neliöiden summa.
Kun kolmion lyhyempien sivujen pituudet ovat a ja b ja pitkän sivun pituus on c, saadaan lause muotoon c2 = a2 + b2. Se voidaan todistaa piirtämällä neljä samanlaista suorakulmaista kolmiota ja sijoittamalla ne niin, että muodostuu suuri neliö ja sen sisään pienempi neliö:

Nyt suuremman neliön pinta-ala ilmoitetaan kahdella tavalla. Koska sen sivun pituus on a + b, ala on (a + b)2. Toisaalta suuren neliön ala saadaan myös lisäämällä keskusneliön alaan kaikkien neljän kolmion alat. Keskusneliön ala on c2, ja kunkin kolmion ala on ½ab, joten ison neliön pinta-alaksi saadaan 4(½ab) + c2. Koska molemmilla tavoilla saatava tulos täytyy olla sama, voidaan kirjoittaa yhtälö:
4(½ab) + c2 = (a + b)2
<=> 2ab + c2 = a2 + b2 + 2ab
<=> c2 = a2 + b2
Muutakin kuin elegantteja todistelmia
Tällaiset hienot todistelmat ovat tyypillisiä esimerkkejä esteettisesti arvokkaista matemaattisista olioista. Mutta on muunkinlaisia.
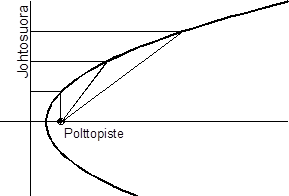
Kuvassa on paraabeli. H. E. Huntley luonnehtii käyrää jo »itsessään kauniiksi», siinä ilmenee »häivähdys äärettömyydestä», mutta lisäulottuvuuden kauneuskokemukseen tuo tieto, että sen periaate on hyvin yksinkertainen: jokaisesta käyrän pisteestä on yhtä pitkä matka johtosuoraan ja polttopisteeseen. Tässä vetoaa »sen ajatuksen yksinkertaisuus, sen menetelmän siisteys, jolla ihastuttava käyrä on saatu aikaan».
Esteettistä arvoa voi olla myös lukujen merkintätavoissa. Vaihtamalla roomalaiset numerot arabialaisiin saadaan usein jokin monimutkaiselta vaikuttanut luku havainnolliseksi tai vaikea laskutoimitus helpoksi. Arabialaista lukujen merkintätapaa voitaisiin tämän nojalla kutsua kauniiksi. Sitä on kehitetty pitemmälle ottamalla avuksi kymmenen potenssit, niin että luku 135 merkitään 1,35 * 102. Etuna on että suurten lukujen »skaala» näkyy selvemmin ja että kertolasku saadaan muuttumaan yhteenlaskuksi ja jakolasku vähennyslaskuksi. Näihin etuihin vedoten Lawrence Krauss puhuu tämän pitemmälle kehitetyn »merkintätavan kauneudesta» ja »luvun kirjoittamisen kauneudesta».
Seuraavana olkoon esimerkki kauniista kaavasta. Sveitsiläinen matemaatikko Leonhard Euler työskenteli Pietari Suuren perustamassa tiedeakatemiassa. Häntä
»viehätti erityisen paljon eräs matemaattinen kaava, jota hän piti kaavoista kauneimpana ja jonka hän hakkautti [Pietarin] akatemian portin päälle. Tämä kaava on // eiπ + 1 = 0 // Kaava on kaunista katseltavaa, mutta siinä on myös monia matematiikan perusasioita: kaavassa on matematiikalle hyvin tärkeä 0, siinä on luku 1, siinä lasketaan yhteen, siinä kerrotaan ja siinä korotetaan potenssiin ja lisäksi siinä ovat imaginaariyksikkö i:n ohella myös irrationaaliset luvut pii (π) ja e.» (Aczel)
Tämä »kaavoista kaunein» voitaisiin kirjoittaa yksinkertaisempaan muotoon: eiπ = –1. Mutta alkuperäisellä muodolla on ansionsa. Yhtälö tuntuu jotenkin lopullisemmalta, kun tuloksena on nolla, ja lisäksi pitemmässä muodossa saadaan mukaan luvut 0 ja 1, jotka ovat »perustavampia» kuin –1. Sen kauneus ei siis niinkään ole äärimmäisessä suppeudessa kuin sen henkimässä lopullisuuden tunnussa ja siinä, että joukko matematiikan perusasioita on saatu tiiviisti yhteen, ikään kuin pienen matemaattisen vesipisaran läpi siintäisi koko matematiikan laaja maailma (tai »matematiikan vaihtelevat maisemat», jos käytetään Walter R. Fuchsin kielikuvaa).
Esteettisesti arvokkaita matemaattisia olioita voivat olla myös lukujoukot. Mainittakoon luvut joita pythagoralaiset nimittivät täydellisiksi, koska ne ovat jakajiensa summia. Luku 6 on jaollinen luvuilla 1, 2 ja 3 ja näiden summa ja siten täydellinen – toisin kuin vaikkapa luku 12, joka on yltäkylläinen, koska sen jakajien summa on 16 (1 + 2 + 3 + 4 + 6), tai luku 10, joka on vaillinainen, koska sen jakajien summa on 8 (1 + 2 + 5). Täydelliset luvut ovat myös ilmaistavissa peräkkäisten kokonaislukujen summina:
6 = 1 + 2 + 3
28 = 1 + 2 + 3 + 4 + 5 + 6 + 7
496 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ... + 30 + 31
8128 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ... + 126 + 127
Jo pythagoralaiset panivat merkille että kaikki 2:n potenssit ovat vain lievästi vaillinaisia:
| potenssi | luku itse | jakajat | jakajien summa | |
| 22 | = 4 | 1, 2 | 3 | |
| 23 | = 8 | 1, 2, 4 | 7 | |
| 24 | = 16 | 1, 2, 4, 8 | 15 | |
| 25 | = 32 | 1, 2, 4, 8, 16 | 31 |
Eukleides esittikin sitten kaavan, jonka mukaan täydelliset luvut ovat kahden luvun tuloja, joissa toinen on 2:n jokin potenssi ja toinen yhtä suurempi 2:n potenssi vähennettynä yhdellä eli kaavana 2n * (2n + 1 – 1) eli esim.
| 6 | = 21 * (22 – 1) |
| 28 | = 22 * (23 – 1) |
| 496 | = 23 * (24 – 1) |
| 8128 | = 24 * (25 – 1) |
Simon Singh kertoo kuinka täydelliset luvut kiehtoivat Pythagorasta, koska ne toisaalta olivat ilmeisen säännönmukaisia mutta toisaalta eivät täysin paljastaneet salaisuuksiaan:
»Pythagorasta kiehtoivat täydellisten lukujen monet säännönmukaisuudet ja ominaisuudet, ja hän ihaili niiden vaikeaselkoisuutta. Täydellisyys näyttää aluksi suhteellisen yksinkertaiselta käsitteeltä, mutta siitä huolimatta antiikin kreikkalaiset eivät kyenneet selvittämään kaikkia sen keskeisiä ongelmia. Vaikka on olemassa useita lukuja, joiden jakajien summa on yksi vähemmän kuin luku itse, jolloin ne siis ovat vain lievästi vaillinaisia, yksikään luku ei silti näytä olevan vain lievästi yltäkylläinen. Kreikkalaiset eivät löytäneet lukuja, joiden jakajien summa olisi ollut yksi enemmän kuin luku itse, eivätkä he osanneet selittää, miksi. Ja vaikka he eivät onnistuneet löytämään tällaisia lievästi yltäkylläisiä lukuja, he eivät toisaalta myöskään osanneet todistaa, ettei sellaisia lukuja ollut olemassa. – – Tällaiset arvoitukset kiinnostivat pythagoralaista veljeskuntaa, eivätkä matemaatikot kykene todistamaan vielä 2500 vuotta myöhemminkään, ettei lievästi yltäkylläisiä lukuja ole olemassa.»
Seuraavaksi hieman toisenlainen lukujen joukko. Huntley puhuu paljon jonosta, joka on ilmeisesti saanut nimensä Leonardo Pisalaisesta, jota kutsutaan myös Bonaccion pojaksi eli filius Bonacciiksi eli Fibonacciksi (noin 1180–1250). Lukujonoa puolestaan kutsutaan Fibonaccin jonoksi, jossa on sanottu olevan »jotain jumalallista». Tässä jonon alkupäästä 21 lukua:
| u0 | 0 | u11 | 89 | |
| u1 | 1 | u12 | 144 | |
| u2 | 1 | u13 | 233 | |
| u3 | 2 | u14 | 377 | |
| u4 | 3 | u15 | 610 | |
| u5 | 5 | u16 | 987 | |
| u6 | 8 | u17 | 1 597 | |
| u7 | 13 | u18 | 2 584 | |
| u8 | 21 | u19 | 4 181 | |
| u9 | 34 | u20 | 6 765 | |
| u10 | 55 | u21 | 10 946 |
Ensimmäiset kaksi lukua ovat 0 ja 1, ja sen jälkeen muut luvut saadaan laskemalla yhteen kaksi edellistä. Yleisessä muodossa tämän jonon periaate on siis un+1 = un + un–1. Huntleyn mukaan »tällä yksinkertaisella jonolla on mielenkiintoisia ominaisuuksia». Yhtenä tällaisena on että perusperiaatteen ohella jono on myös muulla tavoin säännönmukainen. Pannaanpa rinnakkain jonon kymmenen ensimmäistä lukua ja kymmenen lukua lähtien 60. jäsenestä:
| u0 | 0 | u60 | 1 548 008 755 920 | |
| u1 | 1 | u61 | 2 504 730 781 961 | |
| u2 | 1 | u62 | 4 052 739 537 881 | |
| u3 | 2 | u63 | 6 557 470 319 842 | |
| u4 | 3 | u64 | 10 610 209 857 723 | |
| u5 | 5 | u65 | 17 167 680 177 565 | |
| u6 | 8 | u66 | 27 777 890 035 288 | |
| u7 | 13 | u67 | 44 945 570 212 853 | |
| u8 | 21 | u68 | 72 723 460 248 141 | |
| u9 | 34 | u69 | 117 669 030 460 994 |
Huomataan että lukujen viimeiset numerot ovat samoja, ja näin tapahtuu aina 60 jaksoissa. Myös muita kertautuvia sarjoja on viime aikoina löydetty.
Toisena lukujonon »mielenkiintoisena ominaisuutena» mainittakoon yhteys kultaiseen leikkaukseen. Jos seuraava luku jaetaan aina edellisellä, saadaan esim. tällaisia osamääriä:
| 8 / 5 | = | 1,6 |
| 89 / 55 | = | 1,618182... |
| 2 584 / 1 597 | = | 1,618034... |
| 5 702 887 / 3 524 578 | = | 1,618034... |
Huomataan että mitä pitemmälle jonossa edetään, sitä yhtäläisemmiksi osamäärät käyvät: lähestytään itse asiassa kultaisen leikkauksen suhdelukua.

Piste B janalla AC on janan kultainen leikkaus, jos janan AC pituuden suhde janan AB pituuteen on sama kuin jälkimmäisen suhde janan BC pituuteen. Jos janan BC pituus on 1 ja janan AB pituutta merkitään x:llä, voidaan kaava kirjoittaa näin:
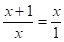
josta saadaan x:n (positiiviseksi) arvoksi
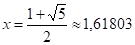
Kun kultaisen suhteen merkkinä käytetään usein kreikan fii-merkkiä (φ), voidaan siis sanoa, että viiden desimaalin tarkkuudella φ on 1,61803. Tätä arvoa Fibonaccin jonon peräkkäisten lukujen osamäärä lähestyy lukujen kasvaessa.
Menemättä tämän pitemmälle lukujonojen ominaisuuksiin tai kultaisen leikkauksen esiintymisyhteyksiin voidaan tiivistää, että kauniit tai esteettisesti arvokkaat matemaattiset oliot voivat olla muutakin kuin todistelmia tai teoreemoja tai laskusuorituksia. Ne voivat olla »ihastuttavia käyriä», tehokkaita lukujen merkitsemistapoja, pieniä mutta laajakantoisia yhtälöitä tai vaikkapa lukujoukkoja, joista löytyy yllättävää säännönmukaisuutta. Oma ryhmänsä on lopulta sekin, missä jokin tuttu asia kuten kultainen leikkaus tai Fibonaccin jono tulee vastaan odottamattomassa paikassa. Huntley kirjoittaa:
»Enemmän kuin miellyttävästä yllätyksestä kohdattaessa odottamatta läheinen ystävä on kyse hämmästyksestä: ›Kuinka ihmeessä sinä olet täällä?!› // Vaikuttaa siltä että matematiikan maailmassa on enemmän risteileviä polkuja kuin olimme uskoneet.»
Tässä kaunis tai esteettisesti kiehtova on oikeastaan itse matematiikan maailma tai sen kolkka, joka tutkimuksen edistyessä paljastuu luultua yhtenäisemmäksi; äkkipäätään kaukaiselta vaikuttavat ilmiöt osoittautuvatkin saman asian muunnelmiksi.
Millaista esteettistä arvoa?
Esteettisesti arvokkaita matemaattisia olioita voivat siis olla muutkin kuin elegantit todistelmat, mutta entä tuo sanaparin ensimmäinen jäsen eli sana ›elegantti›? Huntley kirjoittaa:
»Pilvet ovat yksinäisiä tai vihaisia; aamu on hymyilevä; tammi on majesteettinen; matemaattinen teoreema on elegantti, sen todistus on siisti.»
Pilvet voivat olla myös leppoisia, aamu uhkaava, tammi groteskin epämuodostunut. Entä matematiikka? Voiko se olla esteettisesti arvokasta muuten kuin niiden ominaisuuksien nojalla, joita Huntley kutsuu »matemaattisiksi arvoiksi»: »siisteys, lyhyys, eleganssi ja odottamattomuus, joka voi synnyttää hämmästystä ja jopa tunnun ihmeestä»?
Edellisen esimerkkiaineiston perusteella tekisi mieli lisätä ainakin kiehtova salaperäisyys. Tuntuu hämmästyttävältä että kolme irrationaalilukua e, π ja 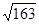 voidaan yhdistää kokonaisluvuksi:
voidaan yhdistää kokonaisluvuksi:
 = 262 537 412 640 768 744
= 262 537 412 640 768 744
Täydellisissä luvuissa puolestaan vetoaa säännöllisyyden yhdistyminen johonkin lopullista selitystä kaihtavaan.
Tällaisista ei ole pitkä matka erilaisiin arvoituksiin ja paradokseihin, vaikkapa todisteluun siitä, kuinka Akhilleus ei voi tavoittaa kilpikonnaa. Matemaatikko Charles Lutwidge Dodgson kirjoitti lastenkirjoja nimellä Lewis Carroll ja laati monia tällaisia paradokseja, joista on sanottu, että »niissä on oma jäljittelemätön sävynsä: sekoitus terävyyttä, kujeilevuutta ja juonikasta viattomuutta» (Newman).
Toinen helposti mieleen tuleva vaihtoehto eleganssille olisi jokin aivan vastakkainen eli vaikkapa koomisuus. Millaista olisi koominen matematiikka?
Ranskassa on julkaistu kymmeniä matematiikan kirjoja, joiden tekijäksi on merkitty Nicolas Bourbaki. Todellisina kirjoittajina ovat Bourbaki-seuran matemaatikot. Nimi seuralle ja kuvitteelliselle kirjoittajalle saatiin ehkä kreikkalaiselta kenraalilta Charles-Denis-Santer Bourbakilta, mutta nimen taustalla oli seuran perustamisen aikaan jo perinteitä:
»– – noihin aikoihin Pariisin yliopiston matematiikan laitoksen perinteisiin kuului kutsua kerran vuodessa joku näyttelijä pitämään luento matematiikasta. Näyttelijä esittäytyi luennon alussa Nicolas Bourbakiksi ja aloitti sitten pitkän yksinpuhelun, joka kuulosti matematiikalta mutta oli todellisuudessa puuta heinää. Ne olivat riemukkaita tilaisuuksia, sillä nykyajan matematiikassa käytetään paljon sellaisia termejä, joiden merkitys on matematiikassa määritelty täsmällisesti mutta jotka tarkoittavat arkipuheessa jotain aivan muuta. // Matemaatikot voivat puhua esimerkiksi kunnan renkaista, mutta he eivät suinkaan tarkoita niillä puhtaanapitolaitoksen kuorma-autojen renkaita. Matematiikan opiskelijat saattaisivat yhtä lailla vääntää vitsejä siitä, mitä sitten tapahtuikaan, kun Akseli Jänne oli onnistunut tekemään treffit Säde Vakion kanssa.»
Näyttelijän yksinpuhelu »kuulosti matematiikalta mutta oli todellisuudessa puuta heinää», mutta yhtä lailla voidaan kuvitella puhe, joka olisi kelvollista matematiikkaa mutta myös järkevää arkikieltä.
Tällainen kaksimielisyys olisi eräällä tavalla koomista matematiikkaa muttei ehkä kovin kiinnostava tapaus. Mieluummin täytyisi löytää rinnasteista hassunkuriselle kompuroinnille tai kaatumiselle, siis todistelmia tai laskusuorituksia, jotka menevät huvittavasti vikaan tai kömpelösti oikein.
On hyvä muistaa että tällainen tahallinen ihanteiden vastaisuus tai pelleily on saanut monia enemmän tai vähemmän institutionalisoituja muotoja matematiikan ulkopuolella. Osmo Meskanen on paitsi monikymmenkertainen Suomen mestari uimahypyssä myös Jerobeam Salakyttä urheiluseurasta Hautausmaan jäykät, ts pellehyppääjä joka jo vuosikymmeniä on pitänyt lajia yllä Suomessa. – Englannissa järjestetään vuosittain Bulwer-Lytton -kilpailu, joissa kamppaillaan huonoimmasta kirjan aloituksesta. Kilpailu on nimetty Edward George Bulwer-Lyttonin mukaan, jonka teos Paul Clifford on alan klassikko ja alkaa: »Oli synkkä ja myrskyinen yö.» – Koiranäyttelyissä etsitään rodun muotovalioita, mutta toisinaan järjestetään myös koirien rumuuskilpailuja, joissa voittaja saattaa olla täysin karvattomaksi muuttunut yksilö. – Saatetaan myöntää palkintoja kauneimmista käsitöistä mutta yhtä lailla vaikkapa maailman huonoimmasta tilkkutäkistä. Vuonna 1997 sen voitti työ, jota ylituomari
»kiittelee – – värisyttävän rumaksi. Siinä on kammottavat värit, täytteet valuvat saumoista ulos, tikkaus on taitamaton ja kääntöpuolikin on kerrassaan hirvittävä.» »Siinä ei ole yhtään pelastavaa ominaisuutta. Se on sotku alusta loppuun. Todellinen suursaavutus.»
Kilpailun voittaja oli alun perin pyrkinyt tosissaan sievään tulokseen, mutta kun asiat alkoivat mennä vikaan, hän päättikin osallistua rumuuskilpailuun. »Minun täytyi purkaa joitakin kohtia, koska työ oli liian hyvää; yritin tehdä kaiken täsmälleen väärin», selitti voittaja onnistumistaan.
Vastaavia esimerkkejä matematiikan alalta ei ole aivan helppo löytää, vaikka siellä tuskin tyritään ja kompuroidaan vähemmän kuin muualla. Matemaatikkojen ei ole tapana julkaista huvittavimpia erehdyksiään. Teekkarihuumorin avaraan syliin mahtuu kuitenkin myös tätä lajia: pyydetään sieventämään lauseke
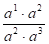
ja vastaukseksi tarjotaan lukua 1/3 (eli on sovellettu sievennyssääntöjä rennolla kädellä ja supistettu kaikki jakoviivan molemmilta puolilta löytyvät samat elementit, vaikka a ei häviä jakoviiva alta minnekään, vaan sievennetty muoto olisi 1/a2).
J. I. Perelman tarjoaa saman tyyppisiä mutta hieman monimutkaisempia esimerkkejä ja puhuu niiden yhteydessä »algebrallisista farsseista» sekä »algebrallisesta huviohjelmistosta». Niissä »virhe – useinkin aivan alkeellinen – on sopivasti naamioitu eikä pistä heti silmään». Eräässä »logaritmisessa komediassa» hän todistaa että 2 on suurempi kuin 3.
Voiko matematiikka olla kaunista?
Kertaan: matematiikan kauneudesta puhutaan yleisesti; esteettisesti arvokkaiksi voidaan kutsua myös muita matemaattisia olioita kuin elegantteja todistelmia; myös väärin tai kömpelösti menevällä suorituksella voi olla oma arvonsa. Yleensä matemaattisesta kauneudesta puhutaan tietysti haltioituneemmassa sävyssä kuin edellisen »huviohjelmiston» yhteydessä. Saatetaan väittää Russellin tavoin, että matematiikassa on »ylintä kauneutta», »kylmää ja karua kauneutta», »riemun todellista henkeä, haltioitumista, tuntua olemisesta jotain enemmän kuin ihminen».
Jos matematiikka yltää kauneuden huipulle, voi tuntua oudolta, että aika usein on myös evätty matematiikan mahdollisuus kauneuteen. Ei tosin ole tavatonta, että alan huipuksi kutsuttu jää joidenkin mielestä koko alan ulkopuolelle. Tieteiden kuningatar matematiikka ei joidenkin mielestä ole tiedettä lainkaan; eivätkä jotkut pidä pelien kuninkaaksi kutsuttua šakkia pelinä lainkaan (vaan matematiikkana). Vastaavasti taiteessa: »Joidenkin mukaan abstraktiset maalaukset eivät ole taidetta ollenkaan ja toisten mukaan ne ovat taiteen huippu.» (Dewey)
Matematiikan mahdollisuus kauneuteen on kielletty sillä perusteella, että se on liian abstraktista. Kylmällä huipullaan se on liian kaukana aistihavainnon ja ihmistunteen lämpimistä laaksoista, joissa esteettisen kukat kukoistavat. 1900-luvun alkupuolella vaikuttanut brittifilosofi W. T. Stace kirjoitti, että »kauniit kohteet ovat luonteeltaan aina pääasiassa havaittavia», ja siksi
»matemaattisia todistuksia ja teoreemoja ei voi – kaikella kunnioituksella Bertrand Russellia kohtaan – tiukasti ottaen kutsua kauniiksi».
Tällaisen kannan taustana on usein ajatus, että »kaunis määrittyy Idean aistittavaksi ilmentymäksi [das sinnliche Scheinen der Idee]», niin kuin Hegel asian ilmaisi. Hegelin jälkiä seuraava marxilainen tutkija saattaa puolestaan sanoa, että kauneus tai kaunis »viittaa esteettiseltä arvoltaan kaikkein arvokkaimpiin ilmiöihin» ja eroaa »moraalisista ja teoreettisista arvoista (hyvästä ja todesta)», koska »siihen liittyy aistittava muoto ja se vetoaa kontemplaatioon tai mielikuvitukseen».
Kun yksi luonnehtii matematiikkaa kauniiksi ja toinen sanoo, ettei matematiikka voi olla kaunista, mistä asiasta nämä ihmiset ovat eri mieltä? Millainen on luonteeltaan kysymys »onko olemassa esteettisesti arvokasta matematiikkaa?»? Se ei ole empiirinen eli kokemusperäinen (niin kuin kysymys »onko olemassa yli kolmimetrisiä ihmisiä?») vaan käsitteellinen. Toisin sanoen kysymys matematiikan kauneudesta ei koske mitään, mikä voitaisiin selvittää tutkimalla maailmaa (edes matematiikan »maailmaa»). Mieluummin kyse on siitä, miten sanaa ›kaunis› tai ilmausta ›esteettisesti arvokas› käytetään, millainen erottelu sen avulla tehdään.
Jos päätetään tai sovitaan, että kauneus liittyy välttämättä johonkin aistittavaan, niin matematiikka ilmeisesti rajautuu ulkopuolelle, koska on samantekevää, millä aistimellisella tavalla todistelma välitetään (puhumalla, painetuin merkein vai sokeainkirjoituksella).
Joku – kutsuttakoon häntä vaikkapa Matemaatikoksi – voisi nyt väittää vastaan sanoen, ettei matematiikka eroa kirjallisuudesta. Ovathan romaanitkin vain ajatusrakennelmia, ja jos kirjallisuutta on luvallista ylistää esteettisesti arvokkaaksi, pitäisi sama kohtelu ulottaa myös matematiikkaan. – Mutta joku perinteisen rajan puolustaja – kutsuttakoon häntä puolestaan Esteetikoksi – voisi vastata: Runoissa äänteellinen ja rytminen osatekijä on usein ensiarvoinen, ja saattaapa olla tärkeää sekin, miltä teksti näyttää sivulla. Myös romaaneissa aistittava puoli on yleensä tärkeä kahdessakin mielessä: 1) ensiksi puhutaan aistittavista asioista (sanotaan »kaide oli kylmän niljakas kuin rupikonnan vatsa» eikä »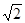 on irrationaalinen»), ja 2) toiseksi teksti on aihetta kuvitella puhutuksi tietyllä tavalla (ikään kuin kertojalle annettaisiin ääni). Olkoon esimerkkinä ensimmäinen virke romaanista Alastalon salissa:
on irrationaalinen»), ja 2) toiseksi teksti on aihetta kuvitella puhutuksi tietyllä tavalla (ikään kuin kertojalle annettaisiin ääni). Olkoon esimerkkinä ensimmäinen virke romaanista Alastalon salissa:
»Kaksitellen ja kolmitellen heitä verkalleen asteli rantamäkeä ylös, välistä useampikin mies yhdessä joukossa, kuinka paatit olivat rantaan saapuneet ja kuinka oli seisoskeltu ja odoteltu muitakin, kun päästelivät purjeitansa alas ja laittelivat venheitänsä jättökuntoon.»
Tässä puheen rytmi on rauhallisesti hengittävä mieluummin kuin ahdistuneen hätäinen. Yhtälö 4(½ab) + c2 = (a + b)2 sen sijaan ei viittaa aistittaviin asioihin eikä siihen ole asiaankuuluvaa kuvitella hengitystä, taukoja tai sanojen raskautta ja keveyttä niin kuin romaanin kerrontaan.
Kaikki tämä ja vielä hieman muutakin voidaan sisällyttää Serge Langin huomautukseen, että »runouden kauneus haalistuu käännettäessä, kun taas matematiikan kauneus pysyy muuttumattomana kielellisissä muutoksissa». Mukaan tulee nimittäin sekin, että sanoilla on käyttöhistoriansa, jonka myötä niihin on saostunut sivumerkitysten paljous, ja siksi ne ovat korvaamattomia. Sitä vastoin matemaattisessa todistelmassa voidaan vaihtaa vaikkapa muuttuja x muuttujaksi w (kunhan muutos tehdään joka kohtaan eikä w:llä ollut mitään aiempaa tehtävää kokonaisuudessa).
Matemaatikko voisi huomauttaa, että nyt mennään jo asiasta sivuun, koska kyse ei ollut käännettävyydestä tai korvattavuudesta vaan sanasta ›esteettinen›. Onko sitä oikeutettua käyttää matematiikasta? Hän voisi perehtyä estetiikan historiaan ja huomata, että aisteista puhuttaessa tarkoitettiin perinteisesti myös tunteita. Hegel saattoi kirjoittaa, että taideteos »on ulkoista ja sisäistä aistitunnetta varten» tai että taiteen kauneus »tarjoutuu aistille, tunteelle, havainnolle, mielikuvitukselle; sillä on toinen ala kuin ajattelulla». Tähän vedoten Matemaatikko voisi sanoa, että koska myös matematiikka herättää tunteita, kuuluu sekin aistimisen ja esteettisen piiriin. Herättihän matematiikka Russellissa »riemun todellista henkeä», ja ranskalainen matemaatikko Henri Poincaré puolestaan kirjoitti:
»Tunneherkkyyteen vetoaminen voi kummastuttaa matemaattisten todistelujen yhteydessä, jotka ehkä näyttävät kiinnostavan pelkästään älyä. Mutta tällöin unohdettaisiin tunne, joka kohdistuu matemaattiseen kauneuteen, numeroiden ja muotojen harmoniaan sekä geometriseen eleganssiin. Kyse on todellisesta esteettisestä tunteesta, joka on tuttu kaikille todellisille matemaatikoille.»
Esteetikko voisi puolestaan huomauttaa, että tässä yhteydessä ei voida vedota kauneuden tunteeseen, koska nimenomaan on tarkoitus selvittää, voidaanko sellaisesta matematiikan yhteydessä puhua.
*
Näin kiista voisi jatkua, mutta kiinnostavampaa tässä yhteydessä on asettaa koko kysymys toisin. Ei kysytä, onko matematiikka siinä määrin aistimellista, että sitä voidaan luonnehtia kauniiksi, vaan kysytään mitä esteettinen olisi siinä kauneuden maailmassa, johon matematiikan kauneus kuuluu itsestään selvänä osana.
Selitän tarkemmin: Kauneuden sitominen aistimellisuuteen on kuulunut lähinnä idealistiseen perinteeseen, jossa ajattelu haluttiin erottaa muista sielun toiminnoista (havaitsemisesta, mielikuvituksesta, tunteista jne), koska vain ajattelemalla kuviteltiin saatavan varmaa tietoa todellisuudesta. Jos ei sitouduta idealismiin, tällainen ajattelun korostaminen ja jyrkkä erottaminen ei tunnu tärkeältä. Ilmaisuja ›kaunis› tai ›esteettisesti arvokas› ei enää tarvitse käyttää erottamaan aistimellisia asioita abstraktisista, eikä siis enää ole käsitteellistä estettä matematiikan kuulumiselle mukaan. Kutsumalla todistelmaa kauniiksi ei sanota mitään sen aistimellisuudesta vaan väitetään sitä esim. itsessään tarkastelun arvoiseksi. Ei siis väitetä, että se on arvokas, koska ongelma on saanut kauan kaivatun ratkaisunsa – ongelma on voitu ratkaista jo aikaa sitten – vaan koska ongelma on ratkaistu vaikkapa erikoisen elegantisti tai hienosti.
Jos ›esteettinen› ei tarkoita aistittavaa, mikä rooli sille voitaisiin antaa? Jos ›kauneus› merkitsee asiaankuuluvaa arvoa ja ›taide› asiaankuuluvaa tekemislajia, mikä jää ›esteettisen› osaksi? Mikä jää sen alaksi, jos matemaattinen kauneus otetaan vakavasti? Perinteisestihän ›esteettinen› on liitetty johonkin toimintoon, jonka on ajateltu olevan kauneuden tajuamisen ehtona. Jos aistiminen ja havaitseminen eivät kelpaa, jääkö mitään tähdellistä jäljelle? Kysymys voidaan muotoilla näinkin: Mitä pitää tehdä tai saavuttaa, jotta matemaattinen todistelma voisi synnyttää »riemun todellisen hengen» tai »tunteen, joka kohdistuu matemaattiseen kauneuteen»?
Ennen kuin vastaan, muistutan siitä laajemmasta kokonaisuudesta, johon kysymys kuuluu. En nyt kysy, mitä sanalla ›esteettinen› on tarkoitettu tai voidaan tarkoittaa, vaan tällä kertaa asetan tiukat alkuehdot: 1) jos matemaattinen kauneus halutaan ottaa mukaan ja 2) jos ›esteettisellä› halutaan tarkoittaa jotain kauneuden tajuamiseen kuuluvaa toimintoa, mikä sen merkitykseksi olisi tarkoituksenmukaista asettaa? Mitä matemaattisen kauneuden tajuaminen vaatii?
Ei riitä että vain ihastellaan paperille muodostuvia vaikean näköisiä merkintöjä, vaan todistelma pitää ainakin jossain määrin ymmärtää. Mutta sekään ei vielä riitä, koska on ymmärtämistä ja ymmärtämistä. Palataanpa aiempaan esimerkkiin Pythagoraan lauseen todistamisesta:
4(½ab) + c2 = (a + b)2
<=> 2ab + c2 = a2 + b2 + 2ab
<=> c2 = a2 + b2
Sulkuja avataan ja yhtälöä sievennetään askel askeleelta, ja jokaisen askelen pitäisi olla viime kädessä palautettavissa aritmetiikan aksiomiin. Kun 4(½ab) saadaan muotoon 2ab, voidaan vedota siihen peruslauseeseen, että mille tahansa luvuille a, b ja k pätee että k * (a * b) = (k * a) * b. Eteneminen voidaan siis pilkkoa pienimpiin mahdollisiin askeleisiin, joista jokaisen pitää olla luvallinen aritmetiikan aksioomien perusteella. Sievennysprosessin pätevyys on siis palautettavissa kunkin askeleen pätevyyteen. Ketju kestää, kun jokainen lenkki kestää. Mitään kuvaa kokonaisuudesta ei tarvitse syntyä. Voimme yhdessä mielessä sanoa ymmärtäneemme todistuksen, kun olemme ymmärtäneet jokaisen päättelyaskeleen, ja päättelyaskeleen ymmärtäminen merkitsee, että näemme sen oikeutetuksi aksiooman perusteella.
Tällaista osa osalta etenevää päättelyä tai ajattelua tai ymmärtämistä on perinteisesti kutsuttu diskursiiviseksi, ja sen vastakohtana on usein pidetty intuitiota. Intuition sijasta voitaisiin tässä yhteydessä puhua yhtä lailla kokonaiskuvasta tai -vaikutelmasta ja sanoa yksinkertaisesti, että todistelman kauneuden tajuaminen edellyttää diskursiivisen ymmärtämisen ohella myös esteettistä ymmärtämistä eli jonkinlaisen kokonaiskuvan muodostumista.
Mikel Dufrenne kutsuu kauniiksi sellaista päättelyketjua, »jota voi seurata kuin melodiaa». Rinnastuksessa on ainakin se itu, että melodian seuraamiseksi ei riitä kuulla, kuinka sävel vaihtuu toiseksi, vaan lisäksi täytyy tajuta, kuinka niistä syntyy kokonaisuus, hahmo. Vastaavasti matemaattisen todistelman kohdalla täytyy tavoittaa taju jostain yhtä päättelyaskelta laajemmasta. Vasta sen jälkeen voidaan arvioida taloudellisuutta, keinojen ja päämäärän suhdetta tms.
Diskursiota on pidetty intuition vastakohtana, koska edellinen on välillistä, jälkimmäinen välitöntä. Tätä välittömyyttä ei kuitenkaan pidä ymmärtää ajallisesti, sillä vaikutelman muodostuminen vaatii aikaa kukkien ja palatsienkin kohdalla, puhumattakaan romaanisarjoista tai satasivuisista todistelmista. ›Välittömyys› merkitsee tässä yksinkertaisesti, että tulokseen ei voi päätyä ikään kuin yhteenlaskun tietä, niin kuin arvosteltaessa päättelyn muodollista pätevyyttä (»koska jokainen askel on pätevä, täytyy kokonaisuudenkin olla pätevä»).
Toinen mielessä pidettävä seikka esteettisen ymmärtämisen yhteydessä on olla asettamatta sitä diskursiivisen ymmärtämisen vastakohdaksi poissulkevassa mielessä. Näinhän saatettiin menetellä René Descartesin vanavedessä, kun erotettiin erilliset (distinctus) mielteet sekavista (confusus) ja suljettiin kauneus jälkimmäiseen karsinaan. Tuloksena oli ajatus, että enkelit eivät voi tajuta kaunista, he kun korkeammin älyllisinä olentoina tajuavat kaiken erillisesti, perimmäisiä yksityiskohtia myöten. Alexander Baumgarten ei tosin tällaiseen sortunut vaan mainitsi myös ymmärryksen kauneuden eli älyllisen kauneuden: ymmärrys (intellectus) kykenee paitsi erottamaan kohteen osat ja piirteet myös yhdistämään ne voimakkaaksi kokonaisvaikutelmaksi eli ekstensiivisesti kirkkaaksi mielteeksi, ja tällöin »täydellisyys on ymmärryksen kauneutta [intellectus pulcritudo]».
Jos pidetään mielessä matemaattisen kauneuden mahdollisuus, pysyy myös ilmeisenä, että diskursiivinen ymmärtäminen ei ole mikään kauneuden tajuamisen este vaan edellytys: todistelman kauneuden tajuaminen jää kovin pinnalliseksi, ellei ymmärretä päättelyaskelten pätevyyttä (tai koomisesti virheellisen kohdalla pätemättömyyttä).
Matematiikan ja taiteen päämääristä
Matematiikkaa ja taidetta ei yleensä mielletä kovin läheisiksi. Siksi tuntuu yllättävältä että kun vuonna 1669 Turun vanhan akatemian ensimmäinen matematiikan professori Simon Kexlerus kuoli, filosofinen tiedekunta päätti ehdottaa hänen seuraajakseen Petrus Laurbecchiusta, runousopin professoria, joka näin saisi »professuurin, joka on arvokkaampi». On kyllä ollut matemaattisesti lahjakkaita runoilijoita Omar Khaijamista Paul Valéryyn, mutta tiedekunnassa tuskin ajateltiin, että nimenomaan runojen tuntija kelpaa opettamaan matematiikkaa.
Taiteen ja matematiikan suhde kokonaisuudessaan on laaja kysymys. Sehän kattaa sekalaisia asioita alkaen intervallien suhteista ja pythagoralaisten lukumystiikasta jatkuen kultaisen leikkauksen esiintymiseen länsimaisessa rakennustaiteessa, taulumaalauksessa tai Joonas Kokkosen Viimeisissä kiusauksissa ja päätyen vaikkapa Iannis Xenakiksen sävellysten perustana olevaan todennäköisyyslaskentaan tai matemaatikkojen taiteellisiin taipumuksiin. Tätä laajaa kenttää en nyt lähde haravoimaan vaan kohdistan huomioni siihen monesti lausuttuun mielipiteeseen, että matematiikka on taiteen kaltaista päämäärältään, koska molemmissa tähdätään esteettiseen arvoon.
Esteettinen päämäärä
Reilut kolme sataa vuotta Kexleruksen jälkeen matematiikan professoriksi Turussa nimitettiin Mats Gyllenberg, joka lausui virkaanastujaisesitelmässään seuraavasti: »Esteettiset aspektit ovat matematiikassa, kuten runoudessakin, ensisijaisen tärkeät.» Matematiikan »esteettinen funktio on pragmaattista funktiota äärettömän paljon tärkeämpi».
On tietysti niitäkin, joiden mielestä »matematiikkaa ei harjoiteta kauneusnäkökohtien vuoksi» (Fuchs), mutta Gyllenbergin tapaan monet muutkin korostavat esteettistä päämäärää. Brittimatemaatikko G. H. Hardy ottaa vertauskohdaksi runouden ohella myös maalaustaiteen:
»Taidemaalarin tai runoilijan tapaan matemaatikko on hahmojen rakentaja. Hänen hahmonsa ovat heidän muodostamiaan pysyvämpiä, sillä ne perustuvat ideoihin. – – Taidemaalarin ja runoilijan tapaan matemaatikon on luotava kauniita hahmoja. Värien ja sanojen tapaan ideoiden on sovittava harmonisesti yhteen. Kauneus on ensimmäinen koe: maailmassa ei ole pysyvää paikkaa rumalle matematiikalle.»
Eräät sovelletun matematiikan alat kuten ballistiikka ja aerodynamiikka saattavat olla hyödyllisiä, mutta ne ovat myös »vastenmielisen rumia ja sietämättömän tylsiä». Sen sijaan todellinen matematiikka, siis
» ›todellisten› matemaatikoiden ›todellinen› matematiikka, Fermat'n ja Eulerin ja Gaussin ja Abelin ja Riemannin ›todellinen› matematiikka on kokonaisuutena täysin ›hyödytöntä› »,
ja siksi »se on oikeutettava taiteena, jos sen ylipäätään voi oikeuttaa».
Poincaré kirjoittaa puolestaan, että ennen muuta matematiikka
»tarjoaa harjoittajilleen samanlaista mielihyvää kuin maalaaminen tai musiikki. He ihailevat lukujen ja muotojen herkkää sopusointua; he ihastelevat, kun uusi keksintö avaa heille odottamattomia näköaloja; ja eikö heidän tällöin kokemansa ilo ole luonteeltaan esteettistä, vaikka aisteilla ei ole siihen mitään osuutta? On totta että vain harvat etuoikeutetut kykenevät nauttimaan siitä täydellisesti, mutta eikö tämä kuulu asiaan ylhäisimpien taiteiden kohdalla?»
Jotkut matemaatikot ovat siis verranneet matematiikkaa taiteeseen, koska molemmissa tavoitellaan esteettistä arvoa. Ovatpa jotkut – lähinnä formalisteiksi luokiteltavat – taidefilosofit puolestaan verranneet taidetta matematiikkaan. Clive Bell korosti että todellisen taiteen tarjoama todellinen mielihyvä – eli se mitä hän kutsuu esteettiseksi emootioksi – on erillään arkielämän huolista ja nautinnoista ja siinä mielessä lähellä matematiikan tuottamaa mielihyvää:
»Tutkimuksiinsa uppoutunut puhdas matemaatikko tuntee tämän mielentilan, joka on nähdäkseni samankaltainen ellei peräti identtinen [sen kanssa jota todellinen taide herättää]. Hän tuntee pohdintojaan kohtaan emootiota, joka ei nouse suhteesta ihmisten elämään vaan (epäinhimillisesti tai yli-inhimillisesti) abstraktisen tieteen sydämestä. Joskus mietin eivätkö taiteen ja matematiikan ihailijat ole vieläkin läheisempää sukua keskenään.»
Tämän suuntaisia yleisiä väitteitä on siis esitetty taiteen ja matematiikan yhtäläisyydestä. Mutta jotta asiasta saataisiin tarkempi kuva, on aihetta kaivautua hieman syvemmälle. Olen valinnut esimerkkitapaukseksi Fermat'n suuren lauseen nimellä tunnetun väittämän.
Sen historia alkaa ehkä jo muinaisesta Babyloniasta, jossa savitauluille kirjoitettiin kolmen luvun ryhmiä niin, että ensimmäinen on kahden seuraavan summa ja lisäksi jokainen luku on kokonaisluvun neliö. Tällaisia ovat luvut 25, 16 ja 9 (52 = 42 + 32) tai 169, 144 ja 25 (132 = 122 + 52). Myöhemmin niitä alettiin kutsua Pythagoraan luvuiksi. Fermat'n »suuren lauseen» mukaan Pythagoraan lukujen tapaisia kokonaislukukolmikoita ei ole olemassa, jos luvut on korotettava suurempaan potenssiin kuin 2. Ts yhtälöllä xn + yn = zn (jossa x, y ja z ovat nollaa suurempia kokonaislukuja) ei ole ratkaisua, jos n on kakkosta suurempi kokonaisluku.
Nimensä lauseelle on antanut 1600-luvulla elänyt ranskalainen lakimies ja matemaatikko Pierre de Fermat, joka ei julkaissut elinaikanaan matematiikan alalta kovin paljon mutta jota silti pidetään 1600-luvun suurimpana ranskalaisena matemaatikkona. Diofantoksen Arithmetika-teos oli vastikään käännetty latinaksi, ja sen reunuksiin Fermat kirjoitti monia huomionarvoisia kommentteja, niiden joukossa »suurta lausetta» koskevan: »Olen keksinyt tähän todella ihmeellisen [mirabilis] todistuksen, mutta sivun reuna on liian kapea sen muistiin merkitsemiseen.»
Arithmetikan reunuksissa oli monia muitakin todistamattomia väitteitä, jotka myöhemmin on onnistuttu todistamaan, mutta »suuri lause» pysyi pitkään liian kovana pähkinänä, vaikka ratkaisuyrityksistä ei ole ollut puutetta:
»Voidaankin sanoa, että kulman kolmijako ja ympyrän neliöinti – – ovat ainoat kysymykset, jotka voivat kilpailla Fermat'n probleeman kanssa harrastelijapiirien suosiosta.» (Kustaa Inkeri)
Vuonna 1908 saksalainen matemaatikko P. Wolfkehl lahjoitti 100 000 silloista Saksan markkaa annettavaksi palkintona probleeman ratkaisijalle. 89 vuotta myöhemmin eli 1997 inflaation olemattomaksi laihduttama palkinto myönnettiin brittiläiselle Andrew Wilesille. Toista vuotta ensimmäisen julkistuksen jälkeen todistus oli supistunut runsaaseen sataan sivuun ja – mikä vielä tärkeämpää – siitä oli saatu poistetuksi alkuperäiseen jäänyt virhe.
Fermat'n »ihmeellinen todistus» – vaikka ei mahtunutkaan kirjan reunukseen – olisi tuskin ollut satasivuinen, ja niinpä etsintä jatkuu. Etsitään lyhyempää ja ehkä samalla elegantimpaa, esteettisempää todistusta. Näinhän matematiikassa yleensäkin menetellään:
»Jo vakiintuneille teoreemoille etsitään uusia todistuksia uhraten paljon työtä, vain koska entiset todistukset eivät miellytä esteettisesti. On olemassa matemaattisia todistuksia, jotka ovat pelkästään vakuuttavia; kuuluisan matemaattisen fyysikon lordi Rayleigh'n sanoin ne ›pakottavat myöntymään›. On toisia todistuksia, ›jotka houkuttelevat ja hurmaavat älyn. Ne synnyttävät iloa ja herättävät ylitsevuotavan halun sanoa aamen, aamen.› Elegantisti toteutettu todistus on runo, paitsi kirjoitusmuotonsa puolesta.» (Kline)
Wilesin todistelmaa on kutsuttu »hyvin monimutkaiseksi» tai jopa »kaikkien aikojen monimutkaisimmaksi»; on sanottu että »vähemmän kuin 10 % lukuteoreetikoista ymmärtää täysin sen logiikan». Mutta sitä on luonnehdittu myös »häikäiseväksi», ja se saattaa olla omalla tavallaan kaunis. Eräs kiehtova piirre on ainakin sen kokonaisuuden laajuus, jonka ongelma ja sen ratkaisu yhdessä muodostavat: jo matematiikan aamuhämärässä alkanut lukukolmikkojen etsiminen synnyttää 1600-luvulla väitteen, jonka todistaminen onnistuu vasta 1900-luvun menetelmin. Todistuksesta on sanottu, että se on »modernin matematiikan täydellinen synteesi» tai jopa että »se kattaa koko matematiikan historian pronssikaudesta nykypäivään saakka».
Vaikka Wilesin todistus siis olisikin omalla tavallaan kaunis, se saattaa »hyvin monimutkaisena» silti kuulua niihin, jotka vain »pakottavat myöntymään». Se ei ole »lyhyt elegantti todistus – – josta matemaatikko näkee, miksi jokin väite on tosi».
*
Matematiikassa siis uhrataan voimia esteettisesti arvokkaan lopputuloksen saavuttamiseksi, ja tässä suhteessa se on taiteen kaltaista.
Toisaalta erojakin on: 1) Ensiksi on hyvä muistaa, että Wiles olisi saanut palkintonsa ja osoittanut olevansa suuri matemaatikko, vaikka hänen todistuksensa olisi esteettisesti surkea. Vaikka pitäisikin paikkansa se Morris Klinen väite, että »todellisen matemaatikon esteettinen taju on vaativampi kuin äkäisin vaimo», ei todistuksen kauneudella ole väliä palkinnon saamisen kannalta. Riittää että todistuksen päätelmät ovat päteviä. Wiles ei saanut palkintoaan koska onnistui hiomaan todistelmansa entistä hienommaksi vaan koska onnistui poistamaan alkuperäiseen todistukseen jääneen virheen. – Tässä mielessä kauneus ei kuulu matematiikan käsitteeseen samalla tavalla kuin taiteen käsitteeseen. Perinteisestihän on ajateltu, että taideteos ei voi olla hyvä taideteos, ellei se ole kaunis eli esteettisesti arvokas: pelkkä moraalinen tai tiedollinen arvo ei riitä nostamaan sitä mestariteosten arvoluokkaan.
2) Toiseksi matematiikka muistuttaa esteettisen päämääränsä puolesta mieluummin voimistelua kuin taidetta. Niin voimistelussa kuin matematiikassa tähdätään vaivattoman vakuuttavaan suoritukseen, eleganttiin ratkaisuun tai tyylikkääseen toteutukseen, vaikka mahdollisuus olisi pyrkiä myös koomiseen kömpelyyteen. Klovnimaista kompastelua ei pidetä hyvänä voimisteluna eikä hyvänä matematiikkana, kun taas näytelmä voi olla hyvä näytelmä, vaikka toiminta olisi koomista, farssimaista tai burleskia.
Taiteen ja matematiikan yhteyttä voitaisiin kuitenkin etsiä myös muiden päämäärien kuin kauneuden suunnalta. Taidehan usein halutaan erottaa eräistä muista kauneuteen tähtäävistä toiminnoista – joulukoristelusta, tulppaanien jalostuksesta tms – sillä perusteella, että taide on tärkeämpää tai syvällisempää. Tätä selitetään edelleen vetoamalla taiteen »totuuteen» tai tiedolliseen arvoon. Nyt voitaisiinkin ajatella, että matematiikka olisi taiteen kaltaista nimenomaan tämän tiedollisen päämäärän osalta.
Tiedollinen päämäärä
Mikä on matematiikan tiedollinen asema? Epäeuklidisen geometrian luomisen myötä kävi ilmeiseksi, että geometria ei ole fysiikan kaltainen luonnontiede. Raymond L. Wilderin sanoin ymmärrettiin, että
»›geometriaksi› kutsuttu matemaattinen järjestelmä ei välttämättä ole todellisen tilan kuvausta – – täytyy erottaa matematiikka ja matematiikan sovellukset.»
Ennen ajateltiin että geometriassa ilmeisistä totuuksista edetään piileviin, mutta jos nykyään ylipäänsä puhutaan totuudesta, tarkoitetaan loogista totuutta eli pätevää päättelyä.
Vaikka ajateltaisiinkin Platonin tavoin, että matematiikka tutkii yhtä todellisuuden lohkoa, nimittäin ideatodellisuutta ja auttaa näin sielua »kääntymään pois syntymisen ja häviämisen piiristä kohti totuutta ja olevaista» tai että »geometria on tietoa ikuisesti olevasta», on ero fysiikan tapaiseen luonnontieteeseen ilmeinen, koska jälkimmäinen keskittyy juuri tähän »syntymisen ja häviämisen piiriin» eli aineelliseen maailmaan.
Epäeuklidisen geometrian esimerkki
Eukleideen Alkeet alkaa 23 määritelmällä, sellaisilla kuin »piste on se, jossa ei ole osia» tai »wiiwa on pituus leweydettä». Tämän jälkeen seuraa viisi postulaattia ja viisi aksioomaa, joiden on tarkoitus olla enemmän tai vähemmän selviöitä, sellaisia kuin »kaikki suorat kulmat owat yhtäsuuret» tai »kokonainen on jokaista osaansa suurempi». Postulaateista viides on ns yhdensuuntaisuuspostulaatti (jota on kutsuttu myös paralleeliaksioomaksi tai paralleelipostulaatiksi), ja sen sisältönä on, että suoran ulkopuolisen pisteen kautta voidaan piirtää yksi ja vain yksi yhdensuuntainen suora.
Tätä postulaattia yritettiin todistaa vuosisatojen ajan, kunnes 1800-luvun alkupuolella tajuttiin, että ristiriidaton geometria voidaan rakentaa myös ilman sitä. Syntyi epäeuklidinen geometria, luojinaan Nikolai Lobatševski Venäjällä, János Bólyai Unkarissa sekä Carl Friedrich Gauss ja Georg Friedrich Bernhard Riemann Göttingenissä.
Oikeastaan syntyi useampia muunnelmia. Lobatševskin ja Bólyain muunnelmassa – jota kutsutaan hyperboliseksi geometriaksi – kolmion kulmien summa on pienempi kuin 180º, ja suoran ulkopuolisen pisteen kautta voidaan piirtää vähintään kaksi yhdensuuntaista suoraa. Riemannin muunnelmassa – jota puolestaan kutsutaan elliptiseksi geometriaksi – ei ole lainkaan yhdensuuntaisia suoria. Kolmion kulmien summa on suurempi kuin 180°.
Epäeuklidisen geometrian myötä tultiin siis tilanteeseen, jossa on erilaisia geometrisia järjestelmiä. Järjestelmät koostuvat aksiomeista (eli postulaateista) ja näihin perustuvista teoreemoista eli lauseista, jotka ovat ehdottoman varmoja tai välttämättömän tosia, koska lause – jos se on todistettu ankaran loogisesti – »yksinkertaisesti lausuu uudelleen osan siitä, mikä postulaateissa stipuloidaan» (Hempel).
Tällaisia geometrisia järjestelmiä voidaan kutsua puhtaiksi, koska niissä ei väitetä mitään todellisuudesta. C. G. Hempel kirjoittaa:
»Puhdas geometria – riippumatta siitä onko se euklidista vai epäeuklidista – ei käsittele mitään aihetta; varsinkaan se ei väitä mitään fysikaalisesta avaruudesta. Kaikki sen lauseet ovat analyyttisia ja siten varmasti tosia juuri siksi, ettei niissä ole tosiasiallista sisältöä. Puhtaan geometrian sisällön luonnehtimiseen voitaisiin käyttää elokuvien alussa toistuvaa kieltoa: Tässä ei ole pyritty kuvaamaan geometristen kuvioiden luonteenpiirteitä eikä todellisten fysikaalisten kappaleiden avaruudellisia ominaisuuksia tai suhteita, ja kaikki yhtäläisyydet alkeiskäsitteiden ja niiden totunnaisten geometristen merkitysten välillä ovat puhtaan satunnaisia.»
Epäeuklidisen geometrian myötä kävi selväksi, että geometria (ja matematiikka yleisemminkin) on jotain muuta kuin luonnontiedettä. Klinen sanoin epäeuklidisen geometrian luominen
»päästi matemaatikon totuuksien sanomisen orjuudesta ja vapautti hänet valitsemaan aksiomeja ja tutkimaan ideoita, joista ei ehkä ole mitään ilmeistä hyötyä fysikaalisen maailman hallitsemisessa tai ymmärtämisessä».
Serge Lang puolestaan kiteyttää:
»Mitä siis fyysikot tekevät? He pyrkivät selvittämään, mitkä mallit sopivat. Mutta matemaatikko – siis puhdas matemaatikko – ei välitä, sopivatko hänen mallinsa vai eivät. Hän rakentaa mukavia malleja, geometrisia malleja, ja jos ne ovat kauniita, sillä on hänelle merkitystä. Hän ei välitä, voidaanko näitä malleja käyttää maailman kuvaamiseen vai ei.»
Sullivan: matematiikka itsetiedostuksen keinona
Jos edellisen mukaisesti ajatellaan että geometria – ja matematiikka yleisemminkin – on irrallaan ulkotodellisuudesta, jos sitä ei pidetä luonnontutkimuksena, niin ehkä sitä tulisi pitää taiteena. Näin päättelee J. W. N. Sullivan:
»Koska matematiikka on täysin vapaata toimintaa, jolle ulkoinen todellisuus ei aseta mitään ehtoja, on oikeudenmukaisempaa kutsua sitä taiteeksi kuin tieteeksi.»
Mutta matematiikan kutsuminen taiteeksi ei Sullivanin mukaan ole sen kutsumista ajanvietteeksi, sillä
»taide ei ole jotain, mikä on olemassa vain tyydyttääkseen ›esteettistä tunnetta›. Nimensä arvoinen taide paljastaa meille jonkin puolen todellisuudesta.»
Kun matematiikka ei suoranaisesti kerro mitään ulkoisesta todellisuudesta, jää jäljelle ihminen itse. Juuri tästä puhuu Sullivanin mukaan niin matematiikka kuin muukin taide. Taiteen »varsinaisena tehtävänä on lisätä itsetuntemustamme, tehdä meidät tietoisemmiksi siitä, mitä olemme» ja niinpä
»matematiikka siinä missä musiikki tai mitkä tahansa muutkin taidelajit on yksi niistä keinoista, joiden avulla kohoamme täydelliseen itsetiedostukseen».
Itse asiassa Sullivanin mukaan matematiikka kertoo mutkan kautta jotain myös meitä ympäröivästä todellisuudesta, sillä »tietoisuutemme ja ulkoinen maailma eivät ole toisistaan riippumattomia», vaan ulkoinen maailma on pitkälti »omaa luomustamme», ja siksi matematiikka »kertomalla mielemme luonteesta kertoo paljosta sellaisesta, mikä riippuu mielemme luonteesta».
Niin taiteen kuin matematiikankin suhde todellisuuteen voitaisiin kuitenkin nähdä myös toisin. Geometrian voitaisiin ajatella tarjoavan mahdollisuuksia, joista sitten valitaan, mikä täsmällisimmin vastaa todellista avaruutta. Tätä vaihtoehtoa esitelläkseni palaan epäeuklidiseen geometriaan.
Taide vaihtoehtojen esittelijänä
Hempel luonnehti edellä geometriaa sanoen, että sen edelle voitaisiin kuvitella samantapainen kielto kuin monien elokuvien edellä, nimittäin että seuraavaksi esitetty ei ole tarkoitettu todellisuuden kuvaukseksi. Hempel kuitenkin jatkaa, että »aivan niin kuin joidenkin elokuvien myös ainakin euklidisen geometrian kohdalla kielto vaikuttaa vähemmän uskottavalta», sillä ›geometria› tarkoitti alunperin maanmittausta, ja
»euklidisen geometrian alkuperä juontuu sellaisten empiiristen löytöjen yleistyksistä ja systematisoinneista, jotka tehtiin alueiden ja tilojen mittaamisen, maanmittauksen ja tähtitieteen yhteydessä».
Niinpä puhtaan geometrian ohella on myös »fysikaalisen avaruuden rakennetta» selvittävä empiirinen opinala, jota Hempel perinteiseen tapaan kutsuu fysikaaliseksi geometriaksi.
Lopuksi hän kysyy, »mikä on puhtaan ja fysikaalisen geometrian suhde», ja vastaa, että »fysikaaliseen geometriaan päästään puhtaan geometrian semanttisen tulkinnan kautta». Tällaisessa »semanttisessa tulkinnassa» päätetään esim. että ›suora› merkitsee valonsäteen kulkureittiä ja ›kolmio› siten kolmen toisiaan leikkaavan valonsäteen rajoittamaa aluetta. Tällaisen tulkinnan jälkeen lause »kolmion kulmien summa on 180º» muuttuu todellisuutta koskevaksi väitteeksi, jota voidaan testata erilaisin koejärjestelyin. Itse asiassa Gauss mittasikin vuorenhuipulta toiselle suunnattujen valosäteiden väliset kulmat ja sai tulokseksi, että mittaustarkkuuden rajoissa niiden summa oli nimenomaan 180º. – Mutta ehkä Gaussin kolmio oli liian pieni. Se avaruuden kaareutuminen, josta yleisessä suhteellisuusteoriassa puhutaan, ei siinä vielä erottunut.
Oli miten oli, epäeuklidisen geometrian eri muunnelmat kehiteltiin ennen kuin oli mitään tietoa niiden mahdollisesta käyttökelpoisuudesta fysiikassa. Hempel:
»Sitä geometrista teoriaa, jota käytetään kuvaamaan fysikaalisen maailman rakennetta, voidaan luonnehtia yleistykseksi elliptisestä geometriasta. Riemann rakensi sen alun perin puhtaan matemaattiseksi teoriaksi vailla mitään välitöntä mahdollisuutta käytännön soveltamiseen. Kun Einstein kehitellessään yleistä suhteellisuusteoriaa etsi sopivaa matemaattista teoriaa fysikaalisen avaruuden rakenteen käsittelemiseksi, hän löysi Riemannin abstraktisesta järjestelmästä tarvitsemansa käsitteellisen välineen.»
Epäeuklidisen geometrian myötä tuli mahdolliseksi kysyä, minkä geometrian mukainen todellisuus on. Ja kun nykytietämyksen valossa vaikuttaa, että todellisuus on epäeuklidinen, nähdään maailma (Oiva Ketosen sanoja käyttäen) »aivan uudella tavalla, todella uutena, uudenlaisena maailmana». – Mutta vaikka todellisuus lopulta olisikin osoittautunut (tai lopulta osoittautuisi) euklidiseksi, oltaisiin silti ratkaisevasti eri asemassa kuin 1700-luvun lopulla, jolloin Immanuel Kantin hengessä saatettiin vielä pitää euklidista geometriaa »ajatusvälttämättömyytenä». On eri asia uskoa, että todellisuus on euklidinen, koska mitään muuta ei voida edes ajatella, kuin uskoa että todellisuus on euklidinen eikä epäeuklidinen, koska kokeet niin osoittavat.
*
Nyt palaan takaisin taiteen ja matematiikan rinnastukseen. Voidaan nimittäin ehdottaa että taiteen suhde todellisuuteen on samantapainen kuin puhtaan geometrian (tai yleisemminkin matematiikan). Molemmissa luodaan kokonaisuuksia, joita sitten voidaan koetella todellisuuteen tai joihin todellisuutta voidaan verrata.
Jotta tämän ajatuksen erityisluonne kävisi selväksi, asetan sen taustaksi perinteisen käsityksen taiteesta jäljittelynä – tai oikeastaan esittelen sen eräitä muunnelmia:
Idealistiset ja heidän vanavedessään marxilaiset filosofit korostivat tyypillisesti, että asian luonteen ymmärtäminen vaatii, että on asettaa jotain sen vastakohdaksi. Yhteiskunnan nykytilan ja ihmisiin kohdistuvan tukahduttamisen voi tajuta vain sellainen, jolla on edes hämärä aavistus paremmasta yhteiskunnasta ja vapaammasta ihmisyydestä. Totuus tammenterhosta on tammi ja totuus tammesta se, millaiseksi se voisi parhaissa oloissa kasvaa. Taide paljastaa piileviä mahdollisuuksia, joita vasten reaalitodellisuuden tila näkyy oikein.
Nämä valaisevat mahdollisuudet voisivat kuitenkin olla paitsi ihanteellisten myös epäihanteellisten tilojen mahdollisuuksia. Tässä hengessä Milan Kundera kirjoittaa Franz Kafkasta. Kafkaahan on pidetty profeettana, koska hänen romaaneissaan on kuvattu tilanteita, jotka monien mielestä toteutuivat myöhemmin Itä-Euroopan totalitaarisissa valtioissa:
»Vallan hypnoottinen katse, oman syyllisyyden epätoivoinen etsintä, sivullisuus ja epäsuosioon joutumisen ahdistus, yhdenmukaisuuteen alistuminen, todellisuuden haamumaisuus ja asiakirjan maaginen todellisuus, yksityisyyden jatkuva loukkaaminen jne., kaikki nämä ihmiskokeet, joita historia valtavissa koeputkissaan on tehnyt, ne kaikki on tehty (muutamia vuosia aikaisemmin) Kafkan romaaneissa.»
Kundera korostaa että Kafkan teosten arvo ei vähenisi, vaikka historia olisikin kulkenut toista tietä. Niiden arvo ei ole kuin sääennustuksen:
»Mutta vaikka hänen romaaneissaan ei olisi mitään profeetallista, ne eivät menettäisi arvoaan, koska niihin on vangittu eräs olemisen mahdollisuus (ihmisen ja hänen maailmansa mahdollisuus) ja koska ne saavat meidät näkemään mitä olemme ja mihin meistä on.» »Romaanikirjailija ei ole historioitsija eikä profeetta: hän on olemisen löytöretkeilijä.»
Näin ajatellen taide näyttää, miten ylös voidaan päästä ja miten alas sortua.
Entäpä abstraktinen, ei-esittävä taide? Nelson Goodman ottaa sen selväsanaisesti mukaan korostaessaan taideteoksille tyypillistä merkitsemisen tapaa, nimittäin esimerkkinä olemista:
»Taideteokset eivät ole mallitilkkuja kangaspakoista tai otoksia tynnyreistä vaan näytteitä merestä. Ne ovat kirjaimellisina tai metaforisina esimerkkeinä muodoista, tunteista, yhtäläisyyksistä, vastakohdista, joita tulee etsiä maailmasta tai rakentaa sinne. Kokonaisuuden piirteitä ei tiedetä, eikä näytteen hyvyydestä voida varmistua ravistamalla tynnyriä tai ottamalla vettä eri paikoista vaan sovittamalla näytteet yhteen. Ts muodon, värin, harmonian oikeellisuus – teoksen hyvyys näytteenä tällaisista piirteistä – tulee koetelluksi siinä, kuinka onnistumme löytämään ja soveltamaan esimerkkinä olevaa. Tapojemme mukaisesti heijastamme todellisuuteen joitain lajeja, jotka kuitenkin muuttuvat uusien kohtaamisten ja uusien ehdotusten myötä, ja juuri tapojemme muuttuminen on mittana yhteensovittamisen onnistumiselle. Mondrianin muoto on oikein, jos se kyetään heijastamaan tehokkaaksi maailman näkemisen rakenteeksi.»
Goodmanin näkemys eroaa edellisistä myös »konstruktiivisuudessaan» eli sen seikan korostamisessa, että kyse ei ole vain löytämisestä vaan myös rakentamisesta tai »maailman tekemisen tavoista» (jos lainataan hänen kuuluisan kirjansa nimeä).
Kaikille näille hieman erilaisille näkemyksille on kuitenkin yhteistä, että taiteen tiedollinen panos seuraa sen jäljittelyluonteesta, mimeettisyydestä. Jokaiseen taideteokseen kuuluisi näin ollen väite »tällaista todellisuus on» tai »tällaisenakin todellisuus voidaan nähdä». Ellei teos varsinaisesti esitä tai kuvaa todellisuutta, se on vähintäänkin näyte todellisuuden merestä, esimerkki »muodoista, tunteista, yhtäläisyyksistä, vastakohdista, joita tulee etsiä maailmasta tai rakentaa sinne».
Jos taas ajatellaan että taiteen suhde todellisuuteen, sen todellisuutta valaiseva tiedollinen rooli on samantapainen kuin matematiikan, täytyy hylätä ajatus mimeettisyydestä. Perinteisestä käsityksestä jää näin jäljelle vain vertailukohdan asettaminen: esitellään jotain samanlaista tai erilaista. Taiteen enempää kuin geometriankaan tehtävänä ei ole näyttää vain, millaista todellisuus on, vaan yhtä lailla, millaista se ei ole. Kumpaankaan ei päde se, mitä Hardy sanoo »sovelletun matemaatikon ajattelusta», nimittäin että sen
»hienoimmat tulokset on hylättävä heti, kun ne on luotu, siitä brutaalista mutta riittävästä syystä, että ne eivät vastaa tosiasioita».
Taiteen ja geometrian ei tarvitse hylätä saavutuksiaan, vaikka ne eivät vastaa todellisuutta.
Tietysti monet taideteokset ja jopa taiteenlajit (kuten muotokuvamaalaus) jäljittelevät mutta taide yleisesti ottaen ei. Siitä että jokin on taideteos ei näin ollen voitaisi päätellä, että teos on ikään kuin kuvaus tai näytepala.
Saattaa hyvin olla (niin kuin Cyril Smith kirjoittaa), että monille ei-esittävän taiteen muodoille on myöhemmin löydetty vastineita luonnosta:
»Kun taiteilijat ovat viimeisen 50 vuoden aikana siirtyneet pois kulttuurisesti määräytyneestä ikonografiasta abstraktiseen tai oletetun ei-esittävään taiteeseen, he ovat tiedostamattaan esittäneet ja joskus ennakoineet sellaisia luonnonmuotoja, joita kehittynein laboratoriotekniikka on paljastanut.»
Mutta tämä ei ratkaise teosten arvoa. Teoksesta ei tee hyvää taidetta, että samantapaisia muotoja tai väriyhdistelmiä löydetään vaikkapa solujen maailmasta. Mieluummin taide ja geometria kartoittaisivat vaihtoehtoja, joista jotkut vastaavat todellisuutta tai soveltuvat todellisuuteen, toiset eivät.
Vaikka sanaa ›taide› käytettäisiin tähän tapaan, tällaisen erottelun tekemiseen, ei tarvitse luopua siitä perinteisestä ajatuksesta, että taiteeseen kuuluu tiedollinen päämäärä. Tämä päämäärä vain ymmärretään väljemmin kuin mimeettisissä taidekäsityksissä. On valaisevaa tajuta myös, millainen todellisuus ei ole. Minimalististen veistosten ankaran geometriset muodot voivat saada meidät kiinnittämään huomiomme johonkin samanlaiseen (johonkin mistä muodot ovat esimerkkeinä), kuten erilaisiin kidemuodostelmiin, mutta yhtä lailla johonkin vastakkaiseen, kuten ameban pyöreään joustavuuteen.
Esimerkkejä ei ole vaikea keksiä esittävänkään taiteen piiristä. Kun saduissa ihminen ymmärtää eläinten puhetta, ei tämän kuvitelman tiedollista arvoa tarvitse perustella viittaamalla yksinomaan kokemuksiin, joissa ihmiset tuntevat olevansa yhtä luonnon kanssa, vaan yhtä lailla myös päinvastaisiin kokemuksiin syvästä vieraudesta, jota eläimet saattavat herättää. Kuvitelma eläinten puheesta korostaa, että todellisuudessa ne eivät puhu. – Vastaavasti lukiessamme George Orwellin romaania Vuonna 1984 voimme huomata niin eroja kuin yhtäläisyyksiä verrattuna nykyaikaan, ja myös erot saattavat olla valaisevia. Voimme oivaltaa, kuinka paljon tehokkaampia ja hienovaraisempia ovat nykyajan valvonta- ja hallintatekniikat kuin romaanissa kuvatut.
sisällysluetteloon
seuraavaan
edelliseen
Viitteet
Schwarz: The Complete Works of Marcel Duchamp, s. 60–61.
Schwarz: The Complete Works of Marcel Duchamp, s. 68; 68; 68.
Osborne: Notes on the Aesthetics of Chess and the Concept of Intellectual Beauty, s. 163; Mathematical Beauty and Physical Science, s. 292.
Lipton & Matthews & Rice: Chess Problems, s. 15; 276; 276.
Lipton & Matthews & Rice: Chess Problems, s. 277; 277.
Kaila & Myllyniemi: Tehtävä- eli taideshakki, s. 1; 12; 12.
Hardy: Matemaatikon apologia, s. 88.
Paul R. Halmos kirjoittaa samassa hengessä: »Matemaatikot myöntävät yleensä vain vastahakoisesti, että šakki on matematiikkaa. He nurisevat, ettei se ole kunnollista matematiikkaa. Matematiikan näkökulmasta šakki on triviaalia. Matematiikkaa šakkipeli kuitenkin on, ja vieläpä puhdasta matematiikkaa.» <Halmos: Soveltava matematiikka on huonoa matematiikkaa, s. 49>
Hardy: Matemaatikon apologia, s. 88; 86; 87.
Salem & Testard & Salem: Kauneimmat matemaattiset kaavat, s. 11.
Aristoteles: Metafysiikka XIII 3, 1078a-b.
Hutcheson: Inquiry into the Original of Our Ideas of Beauty and Virtue, Treatise I Section I Article IX; Treatise I Section II Article III.
Hutcheson: Inquiry into the Original of Our Ideas of Beauty and Virtue, Treatise I Section II Article III.
Hutcheson: Inquiry into the Original of Our Ideas of Beauty and Virtue, Treatise I Section III Article III.
Hutcheson: Inquiry into the Original of Our Ideas of Beauty and Virtue, Treatise I Section III Article I.
Hutcheson: Inquiry into the Original of Our Ideas of Beauty and Virtue, Treatise I Section III Article V.
Eukleides: Euklideen Alkeista kuusi ensimmäistä kirjaa, s. 48–49.
Russell: The Study of Mathematics, s. 86–87.
Papanek: Turhaa vai tarpeellista? s. 39–40.
Toinen esimerkki vaikean tekemisestä helpoksi: »Opettajien kiusaamat opiskelijat eivät ole nykyajan ilmiö, vaikka jotkut haluaisivat meidän luulevan niin. Vuonna 1787, esimerkiksi, luokassaan vallitsevaa kaaosta kauhistunut opettaja päätti rangaista oppilaita pakottamalla heidät laskemaan sadan ensimmäisen kokonaisluvun summan // 1 + 2 + ... + 100 // Rauhallista lopputuntia ennakoinut opettaja istahti levähtämään. Hänen kannaltaan valitettavasti eräs oppilas, Karl Friedrich Gauss, ilmoitti miltei heti, että oli saanut summan valmiiksi ilman ainuttakaan laskutoimitusta. // ›Tämä on hyvin yksinkertaista›, hän selitti. ›Jos kirjoitan summan päinvastaisessa järjestyksessä alkuperäisen alle – – ja lasken luvut yhteen, saan tehtäväksi annetun summan kaksinkertaisena. Mutta 1 + 100 = 2 + 99 = 3 + 98 = ... = 101. Laskemalla ›alekkain› saan luvun 101 sata kertaa.› Niinpä tulos on ½ * 100 * 101 = 5050.» <Salem & Testard & Salem: Kauneimmat matemaattiset kaavat, s. 92>
Huntley: The Divine Proportion, s. 70; 71; 71.
»Tieteellisellä merkintätavalla – – jokainen luku voidaan kirjoittaa lukujen 1 ja 10 välissä olevaksi luvuksi kerrottuna luvulla, jossa ykköstä seuraa n nollaa. Luku 100 on 102, kun taas luku 135 on 1,35 * 102. Tämän merkintätavan kauneus on siinä, että sen toisen osan eksponentti eli kymmenen potenssi kertoo välittömästi luvun sisältämien nollien määrän eli sen ›kymmenen kertaluvun› (niinpä lukujen 100 ja 135 kertaluku on sama), kun taas ensimmäinen osa kertoo, mikä arvo luvulla on tässä suuruusluokassa (eli siis onko se 100 vai 135).» »Jos laskee nollat oikein, tulo 100 * 100 osoittautuu olevan 10 000. Jos sen sijaan kirjoitetaan 102 * 102 = 10(2 + 2) = 104, kertolasku muuttuu yhteenlaskuksi. Vastaavasti kirjoittamalla 1000 / 100 = 10 muotoon 103 / 102 = 10(3 - 2) = 10, jakolasku muuttuu vähennyslaskuksi. Kymmenen potenssien laskusääntöjen avulla laskutoimituksen keskeinen vaikeus, sen suuruusluokan määrittäminen, muuttuu itsestäänselvyydeksi.» »Luvun 1,4960 * 1011 kaltaisen luvun kirjoittamisen kauneus on siinä, että sen tarkkuuden näkee heti, koska kerroin 1011 määrittää luvun ›skaalan›. Mitä enemmän desimaaleja lukuun kirjoitetaan, sitä tarkempi se on.» <Krauss: Oleta pyöreä lehmä, s. 44, 45, 49>
Aczel: Fermat’n teoreema, s. 59–60. Olen korjannut loppuosaa, sillä alun perin siinä luki »luonnolliset luvut pii (π) ja e».
Singh: Fermat’n viimeinen teoreema, s. 34–35.
Aczel: Fermat’n teoreema, s. 49.
Huntley: The Divine Proportion, s. 141.
Olkoon tässä vielä yksi esimerkki lukujoukon kiehtovasta säännönmukaisuudesta. Luku 12345679 kerrottuna 12:lla antaa tulokseksi 148 148 148, luvulla 39 481 481 481 ja luvulla 66 814 814 814. Seuraavassa ilmiön analyysia:
12345679 * 12 = 37/3 * 1001001 * 12 = 37/3 * (3 * 4) * 1001001 = 148 * 1001001 = 148148148.
Huntley: The Divine Proportion, s. 142–143.
Huntley: The Divine Proportion, s. 14.
Huntley: The Divine Proportion, s. 149.
Gideon Engler huomauttaa että tieteen yhteydessä käytetään melko harvoja esteettisiä termejä: »– – tieteessä terminologia ei ole juuri runsaampi kuin: ›elegantti›, ›nätti›, ›siisti›, ›tylsä›, ›kömpelö›, ›ruma›, ja näidenkin käyttö on suppeaa. Esim. ›nättiä› tai ›siistiä› käytetään yleensä tarkoituksena korostaa jonkin keinon tehokkuutta, kun tarkoitus on päästä matemaattisen suhteen ›eleganttiin› todistukseen.» <Engler: Aesthetics in Science and in Art, s. 32–33>
Asiaa oli ounastellut jo Srinivasa Ramanujan, mutta todistuksen esitti John Brillo 1974.
Newman: Commentary on Lewis Carroll, s. 2397.
Aczel: Fermat’n teoreema, s. 101–102.
Lainaukset ovat Pirkko Kuosmasen artikkelista »Maailman huonoin tilkkutäkki valittiin viimeisen kerran» (Helsingin Sanomat 2.12.1997, s. D8) ja Internet-sivulta osoitteesta
http://ttsw.com/artists/worstquilt97/worstquilt97.html.
Kootut äpyt, s. 12. Porvoo 1990.
Perelman: Kiintoisaa algebraa, s. 167; 165; 165.
Perelman: Kiintoisaa algebraa, s. 250–251.
Russell: The Study of Mathematics, s. 86.
Dewey: Art as Experience, s. 93.
Stace: The Meaning of Beauty, s. 11–12; 13.
Hegel: Vorlesungen über die Ästhetik, Bassenge I s. 117/ Knox I s. 111.
Lang: The Beauty of Doing Mathematics, s. 18.
Hegel: Vorlesungen über die Ästhetik, Bassenge I s. 45/ Knox I s. 35; Bassenge I s. 17/ Knox I s. 5.
Poincaré: Science et Méthode, s. 57; Science and Method, s. 59.
Dufrenne: Phénoménologie de l’expérience esthétique, s. 21.
Asiasta mainitsee esim. Riemann: Die Ästhetik Alexander Gottlieb Baumgartens, s. 35.
Baumgarten: Metaphysica, §637.
Lehti: Matematiikan tulo Suomeen yliopistolliseksi oppiaineeksi, s. 146. Lainaus on konsistorin päätöksestä.
Gyllenberg: Matematiikka luonnontieteiden kielenä, s. 231; 232.
Hardy: Matemaatikon apologia, s. 84–85.
Hardy: Matemaatikon apologia, s. 141; 120; 140.
Poincaré: La valeur de la science, s. 139; The Value of Science, s. 75–76.
Suomennos on Kustaa Inkerin: Fermat’n probleema, s. 27. Alkukielellä: »Cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.» <Fermat: Oeuvres I, s. 291>
Inkeri: Fermat’n probleema, s. 24.
Simon Sing kirjoittaa: »Muut matemaatikot, romanttiset optimistit, sen sijaan uskovat, että Fermat oli ehkä sittenkin keksinyt aidon todistuksen. Mutta olisipa se ollut millainen tahansa, se olisi joka tapauksessa perustunut 1600‑luvun menetelmiin, ja sen päättelyn olisi pitänyt olla niin ovelaa, että se olisi jäänyt huomaamatta kaikilta Eulerista Wilesiin. Wilesin ratkaisun julkaisemisesta huolimatta monet matemaatikot uskovat vieläkin voivansa saavuttaa mainetta ja kunniaa keksimällä Fermat’n alkuperäisen todistuksen.» <Singh: Fermat’n viimeinen teoreema, s. 336–337>
Kline: Mathematics in Western Culture, s. 524.
Aczel: Fermat’n teoreema, s. 149; Singh: Fermat’n viimeinen teoreema, s. 297; Singh: Fermat’s Last Theorem, s. 327.
Aczel: Fermat’n teoreema, s. 22. Viimeisen pulman ratkaisu oli Wilesin omien sanojen mukaan »niin käsittämättömän kaunis, niin yksinkertainen ja niin tyylikäs... että minä vain tuijotin sitä uskomatta silmiäni». <Aczel: Fermat’n teoreema, s. 146; lähes samoin sanoin myös Singh: Fermat’n viimeinen teoreema, s. 326>
Singh: Fermat’n viimeinen teoreema, s. 332: Aczel: Fermat’n teoreema, s. 127.
Hannele Salminen & Jouko Väänänen: »Tietokone laski ratkaisun, kun ihminen ei osannut». Helsingin Sanomat 21.12.1996 s. D2.
Wilesin todistusta selvempi esimerkki monimutkaisesta todistuksesta olisi tietysti jokin sellainen, josta Salminen ja Väänänen artikkelissaan puhuvat: tietokone laskee tulosta viikon; sen oikeellisuudesta ihmiset eivät osaa sanoa mitään, joten toinen ohjelma pannaan tarkastamaan sitä.
Nimenomaan matematiikan hyödyttömyys tekee esteettisen arvon tärkeämmäksi matematiikassa kuin monissa muissa ihmisen pyrinnöissä. Tässä yhteydessä kannattaa muistaa Francis Guthrien ongelma: Tarvitaanko minkään kartan alueiden värittämiseen enempää kuin neljä väriä, niin ettei samaa väriä koskaan ole rajan kahden puolen? 1976 Wolfgang Haken ja Kenneth Appel todistivat tietokonetta käyttäen, että ei tarvita. Tätä todistusta ihmiset eivät enää kykene tarkistamaan, ja tarkistusmielessä ohjelma ajettiin läpi toisessa tietokoneessa samoin tuloksin. Tällainen todistus saattaa lisätä tietoa muttei ymmärrystä, eikä se ainakaan voi olla ihmisille esteettisesti arvokas, koska sitä ei voida esteettisesti ymmärtää eli siitä ei voida saada kokonaisvaikutelmaa. Philip Davis kirjoittaakin reaktiostaan: »Ensimmäinen ajatukseni oli: ›Mainiota, miten he sen tekivät?› Odotin jotain loistavaa uutta oivallusta, todistusta jonka ytimenä olisi sävähdyttävän kaunis idea. Mutta vastauksena oli: ›He jakoivat sen tuhansiksi tapauksiksi ja ajoivat kaikki tietokoneessa, yhden toisensa jälkeen.› Olin masentunut ja ajattelin: ›Niinpä se ei siis ollutkaan hyvä ongelma.› » <Singh: Fermat’s Last Theorem, s. 329>
Kline: Mathematics in Western Culture, s. 524.
Wilder: The Axiomatic Method, s. 1650.
Eukleides: Euklideen Alkeista kuusi ensimmäistä kirjaa, s. 5–13.
Suomennetussa versiossa ei postulaatteja ole kuin kolme. Viides postulaatti on paikallaan esim. englanninkielisessä versiossa The Thirteen Books of Euclid’s Elements 1 s. 155.
Hempel: Geometry and Empirical Science, s. 1638. Hempel kirjoittaa myös: »Matematiikan väitteillä on siksi sama kiistaton varmuus, joka on tyypillistä sellaisille väitteille kuin ›kaikki poikamiehet ovat naimattomia› – –.» <On the Nature of Mathematical Truth, s. 1631>
Hempel: Geometry and Empirical Science, s. 1641–1642.
Kline: Mathematics in Western Culture, s. 520.
Lang: The Beauty of Doing Mathematics, s. 74.
Sullivan: Mathematics as an Art, s. 2020.
Sullivan: Mathematics as an Art, s. 2020–2021.
Sullivan: Mathematics as an Art, s. 2021; 2021.
Sullivan: Mathematics as an Art, s. 2021; 2021; 2021.
Hempel: Geometry and Empirical Science, s. 1642; 1642; 1642.
Hempel: Geometry and Empirical Science, s. 1642; 1642.
Hempel: Geometry and Empirical Science, s. 1646.
Ketonen: Suuri maailmanjärjestys, s. 379.
Kun tähän tapaan puhun todellisuudesta, kyse on tietenkin muusta kuin platonisesta ideatodellisuudesta.
Kundera: Romaanin taide, s. 121.
Kundera: Romaanin taide, s. 50; 51.
Goodman: Ways of Worldmaking, s. 137.
Hardy: Matemaatikon apologia, s. 135–136.
Vaikka en asiaa tässä erityisesti korosta, kyse on siis kaiken aikaa käsitteellisestä erottelusta tai ehdotuksesta, jonka mukaan jonkin väittäminen taiteeksi ei merkitsisi väitettä sen jäljittelevästä suhteesta todellisuuteen.
Smith: Structural Hierarchy in Science, Art, and History, s. 21–22.

 , // joka on kiistattomasti oikea. Tämän jälkeen seuraa muunnos //
, // joka on kiistattomasti oikea. Tämän jälkeen seuraa muunnos // 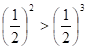 , // joka ei myöskään herätä epäilyksiä. Suurempaa lukua vastaa suurempi logaritmi, ja siis //
, // joka ei myöskään herätä epäilyksiä. Suurempaa lukua vastaa suurempi logaritmi, ja siis // 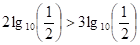 ; Supistettuamme luvulla
; Supistettuamme luvulla 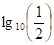 saamme: 2 > 3. – – Virhe on siinä, että supistettaessa luvulla
saamme: 2 > 3. – – Virhe on siinä, että supistettaessa luvulla 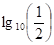 ei erisuuruusmerkin suuntaa vaihdettu (> ja <); kuitenkin se on tehtävä, koska
ei erisuuruusmerkin suuntaa vaihdettu (> ja <); kuitenkin se on tehtävä, koska 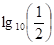 on negatiivinen luku.»
on negatiivinen luku.»